What the Factored Form of a Quadratic can tell you about the graph
Like standard and vertex forms, the factored form of a quadratic function:
y = a · (x - c) · (x - d)
can also tell you whether the given quadratic has a graph that “smiles†or “frowns.†As
with the standard and vertex forms the key again is the sign (+ or -) of the number a. If a
is positive the graph “smiles†and if a is negative the graph “frowns.†Sometimes you
will see an example of a factored form that does not appear to have a value of a, such as:
y = (x -1) · (x + 2).
In this case, the value of a is equal to one (which is positive) and the graph of the
quadratic will smile.
The factored form of a quadratic equation also tells you where the x-intercepts
(sometimes called the roots or zeros of the quadratic function are located). The xintercepts
of the equation are the x-values that will make y = 0.
For example, the x-intercepts of the quadratic:
y = (x -1) · (x + 2)
are x = 1 and x = -2 as plugging either of these two values into the quadratic equation
will make y equal to zero.
Example
Figure 1 shows the graph of a quadratic function. Find the equation of
this quadratic and express your answer in both factored and standard forms.
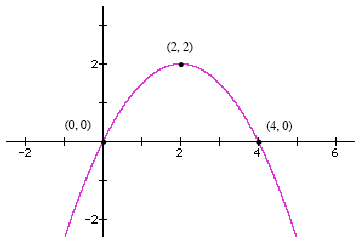
Figure 1: Find the formula of this quadratic function.
Solution
Figure 1 clearly shows both the of the x-intercepts of the quadratic function so it will be
easiest to find the factored form of the quadratic first and then convert this to standard
form by FOILing.
The x-intercepts of the quadratic shown in Figure 4 are located at x = 0 and x = 4. This
means that the factored form of the quadratic function must look something like this:
y = a · (x - 0) · (x - 4) = a · x · (x - 4) .
The factored form must have a factor of (x - 0), or more simply a factor of just x, to
ensure that when you plug in x = 0 the value of y will be equal to zero. The factored form
must also have a factor of (x - 4) to ensure that when you plug in x = 4 the value of y will
be equal to zero.
To determine the numerical value of a you can plug in the x- and y-coordinates of any
other point on the quadratic graph (i.e. any point other than one of the x-intercepts) and
solve for a. Figure 1 shows that the point (2, 2) lies on the graph, so you can plug in x =
2 and y = 2 into the factored form. Doing this:
2 = a · 2 · (2 - 4)
2 = a · (-4)
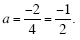
So, the equation of the quadratic function from Figure 1 (written in factored form) is:
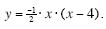
To convert this equation to standard form, you can expand by FOILing and then simplify
(if necessary). Doing this:
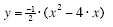 (Expand by FOILing) (Expand by FOILing)
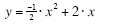 (Multiply through by (Multiply through by
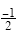 - beware of “-†signs) - beware of “-†signs)
The formula for the quadratic shown in Figure 1 (expressed in standard form) is:
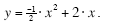
|
