Inequalities with Fractions
Inequalities with fractions are solved in a similar manner as
quadratic inequalities.
EXAMPLE
Solve 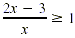 . .
Solution
First solve the corresponding equation.
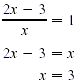
The solution, x = 3, determines the intervals on the number
line where the fraction may change from greater than 1 to less
than 1. This change also may occur on either side of a number
that makes the denominator equal 0. Here, the x-value that makes
the denominator 0 is x = 0. Test each of the three intervals
determined by the numbers 0 and 3.
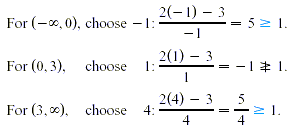
The symbol 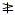 means “is not greater than or equal
to”. Testing the endpoints 0 and 3 shows that the solution
is means “is not greater than or equal
to”. Testing the endpoints 0 and 3 shows that the solution
is 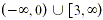 . .
CAUTION
A common error is to try to solve the inequality in the
previous example by multiplying both sides by x. The reason this
is wrong is that we don’t know in the beginning whether x is
positive or negative. If x is negative, the 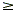 would change to
would change to 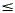 according to one of the properties of
inequalities. according to one of the properties of
inequalities.
EXAMPLE
Solve 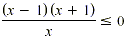
Solution
Solve the corresponding equation.
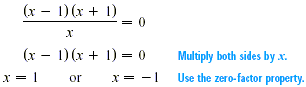
Setting the denominator equal to 0 gives x = 0, so the
intervals of interest are 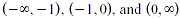 . Testing a number from each region in the original
inequality and checking the endpoints, we find the solution is . Testing a number from each region in the original
inequality and checking the endpoints, we find the solution is 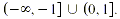
CAUTION
Remember to solve the equation formed by setting the
denominator equal to zero. Any number that makes the denominator
zero always creates two intervals on the number line. For
instance, in the previous example, 0 makes the denominator of the
rational inequality equal to 0, so we know that there may be a
sign change from one side of 0 to the other (as was indeed the
case).
EXAMPLE
Solve 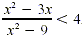 . .
Solution
Solve the corresponding equation.
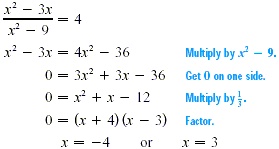
Now set the denominator equal to 0 and solve that equation.
x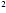 - 9 = 0 - 9 = 0
(x + 3)(x - 3) = 0
x = 3 or x = -3
or The intervals determined by the three (different) solutions
are 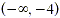 , , 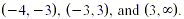 Testing a number from each interval in
the given inequality shows that the solution is Testing a number from each interval in
the given inequality shows that the solution is
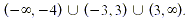
For this example, none of the endpoints are part of the
solution because x = 3 and x = -3 force the denominator to be
zero and x = -4 produces an equality.
|
