Laws of Exponents and Dividing Monomials
What happens when we divide powers? Let's analyze this by
dividing various powers of 2.
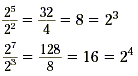
Try to make a conjecture about dividing powers that have the
same base.
In both cases, the result is the original base raised to the
power given by the difference of the two exponents.
For , 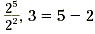
and for 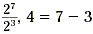 . .
The table on the left shows what happens when a power of 2 is
divided by 2 1 . The table on the right shows what
happens when a power of 2 is divided by 2 2

In the table on the left, notice the powers that result. Each
resulting power can be found by subtracting 1 from the exponent
of the original power. In the table on the right, each resulting
power can be found by subtracting 2 from the exponent of the
original power. This agrees with our original observation that
when we divide two powers with the same base, the exponent of the
resulting power is the difference of the exponents of the two
dividends.
Consider another case. Let's divide a 4 by a 2.
To do this, expand a 4 into a · a · a · a and a
2 into a · a . Next place them into the fraction
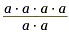
We can now cancel two a's from both numerator and denominator.
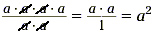
Cancellation is a shorthand process involving the properties
of fractions. Also, point out that any number raised to the first
power is that number itself.
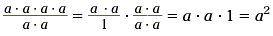
After canceling, we find that 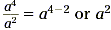 . .
In general, when we write the quotient and expand it into
products of a's, the result is
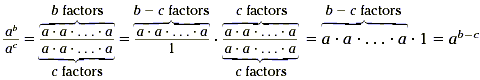
which shows why this fact is valid.
Key Idea
When we divide a power of a by another smaller power of a ,
the result is a power of a , in which the exponent is the
difference of the exponents of the two dividends. In symbols,
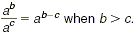
This holds true for any nonzero number a and whole numbers b
and c.
|
