Radicals
We have defined 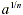 as the positive or principal nth root of a for
appropriate values of a and n. An alternative notation for as the positive or principal nth root of a for
appropriate values of a and n. An alternative notation for 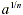 uses
radicals. uses
radicals.
RADICALS
If n is an even natural number and a > 0 or n is an odd
natural number, then
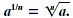
The symbol 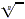 is a radical sign, the number a is the radicand, and
n is the index of the radical. The familiar symbol is a radical sign, the number a is the radicand, and
n is the index of the radical. The familiar symbol 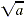 is used
instead of is used
instead of 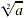 . .
EXAMPLE 1
Radical Calculations
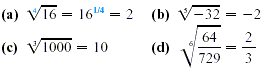
With 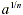 written as written as 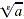 , , 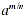 also can be written using radicals. also can be written using radicals.
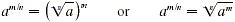
The following properties of radicals depend on the definitions
and properties of exponents.
PROPERTIES OF RADICALS
For all real numbers a and b and natural numbers m and n such
that 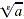 and
and 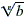 are real numbers:
are real numbers:
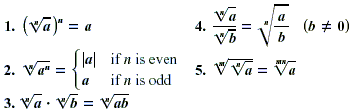
Property 3 can be used to simplify certain radicals. For
example, since 48 = 16·3,
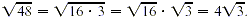
To some extent, simplification is in the eye of the beholder,
and 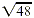 might be considered as simple as
might be considered as simple as 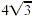 . In this
textbook, we will consider an expression to be simpler when we
have removed as many factors as possible from under the radical. . In this
textbook, we will consider an expression to be simpler when we
have removed as many factors as possible from under the radical.
EXAMPLE 2
Radical Calculations
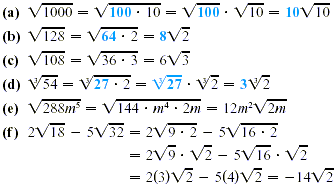
|
