Ratios
A ratio compares two amounts. You can use ratios to compare numbers in different ways. For
instance, you can compare part of a group to the whole collection:
"Four out of five kids like math!"
Or, you can compare part of a group to another part:
"For every four kids that like math, one more kid doesn't."
A ratio is the relationship between two numbers or values.
Writing Ratios in Simplest Terms
When the numbers in a ratio are large, it can be difficult to see the relation between them. It
often helps to reduce a ratio to its simplest terms.
To write a ratio in simplest terms, divide both parts by their greatest common factor (GCF).
Reducing a ratio to simplest terms does not change the relationship between the numbers.
Suppose a ratio of chocolate donuts to maple bars is 6:4. Notice there are three chocolate
donuts for every two maple bars. We can reduce the ratio 6:4 to 3:2.
Reducing a ratio is very much like reducing a fraction.
Common Mistakes With Ratios
ØWarning: A common mistake with ratios is in choosing the term for the ‘total’. Read the
problem carefully! Does it ask to compare a number to the total amount, or to the
remaining
amount?
Tying Them All Together
Ratios and fractions are interchangeable, and they can also be written as a decimal or a percent.
| Percent |
Decimal |
Fraction |
Ratio |
| 6% |
0.06 |
6/100 |
0.06 : 1
or 3 : 50 |
Identifying Equal Ratios
Since a ratio is just another fraction, multiplying or dividing both terms by the same number does
not change the ratio.
Example:
Are the ratios
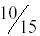and
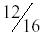equal?
Solution 1: Equivalent Fractions
 common denominator =
12
So re-write the fractions using the common denominator:
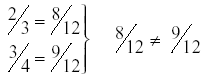 ratios are not equal
Solution 2: Cross Product Test
Another way to compare ratios or fractions is to use the cross product test:
This is usually the easiest way to compare fractions at a glance.
Multiply the numerator of one fraction by the denominator of the other. Do this
for both fractions, and write the answers. If the two products are equal, then
the fractions are equal.
 ratios are not equal
Here’s another neat thing about the cross product test. It can easily tell you
which fraction is larger! Just write the product above its numerator. Then
compare the numbers in the same order you wrote them. For example:
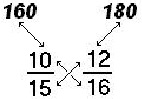 the right hand ratio is larger
Solution 3: Decimal Comparison
Another way to compare ratios is to grab your calculator, and compute the
decimal number.
10/15 = 0.6666666666667
12/16 = 0.75 ratios are not equal
|
