Adding and Subtracting Rational Expressions
Definition A rational expression is a ratio
(fraction) of two polynomials. All rational expressions are valid
for all real numbers except those values that make the
denominator zero.
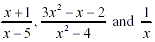 are rational expressions whereas are rational expressions whereas 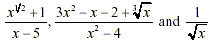 are not. are not.
When adding (or subtracting) rational expressions with a
common denominator, the process is straightforward: Simply add
(or subtract) the numerators, and put the result in a rational
expression with the same denominator; i.e.,
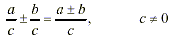
where a, b and c are polynomials.
Example 1
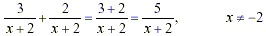
Example 2
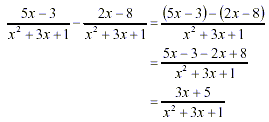
Note that there is no restriction on x because 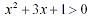 , as will be shown in another paper. , as will be shown in another paper.
When performing any operation with rational expressions of a
single variable, we must make sure our final answer is
simplified:
a. All polynomials are in descending order; i.e., the largest
power of the variable appears on the left and as we proceed to
the right, the powers of the variable decrease.
b. All leading terms (highest degree terms) in the denominator
have positive coefficients.
c. All like (similar) terms have been combined.
d. The greatest common factor of the numerator and denominator
is 1; i.e., all common factors have been divided out.
e. Unless told otherwise, the numerator is to multiplied out
and simplified, while the denominator may be left in factored
form.
The expressions, 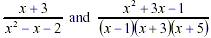 , are considered to be simplified. The
expressions, , are considered to be simplified. The
expressions, 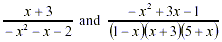 are not considered to be simplified. The
following shows how to convert the latter pair of expressions
into simplified forms. are not considered to be simplified. The
following shows how to convert the latter pair of expressions
into simplified forms.
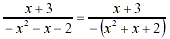 [Factor out -1 from denominator] [Factor out -1 from denominator]
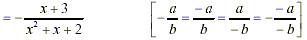
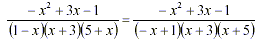 [Put in descending order] [Put in descending order]
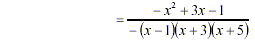 [Factor out -1 from (-x + 1)] [Factor out -1 from (-x + 1)]
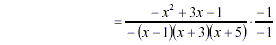 [Eliminate the leading neg sign in
denom.] [Eliminate the leading neg sign in
denom.]
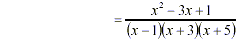 [Simplify] [Simplify]
Example 3
Substract: 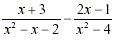
Solution: The factorizations of the
denominators are
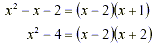
Hence the LCD is:
LCD = (x - 2)(x + 2)(x + 1)
Use these factorizations to convert the rational expressions
to rational expressions that have the LCD for their denominators,
perform the subtraction, and simplify the result.
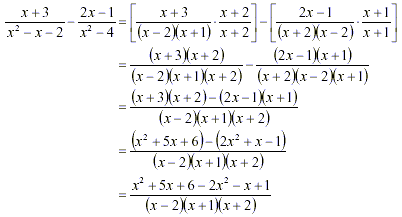
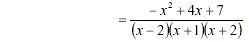 [Acceptable as being simplified] [Acceptable as being simplified]
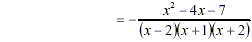 [Preferrable] [Preferrable]
Note that the above is valid for all 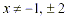 . What this means is that if we
substitute any value of . What this means is that if we
substitute any value of 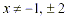
into 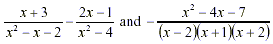 , and evaluate the expressions, we obtain
the same result. , and evaluate the expressions, we obtain
the same result.
For example, let x = 3. Then we obtain
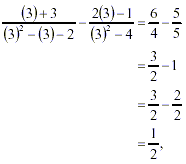
and
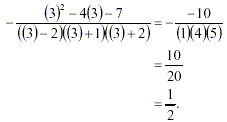
|
