Adding, Subtracting, and Finding Least Common Denominators

Recall: When you add or subtract fractions with like denominators, you combine the tops and leave the bottoms alone. Of course, you reduce to lowest terms when you’re done.

Examples:

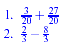
New Stuff:

• Adding rational expressions with like denominators

Procedure: (Adding Rational Expressions with Like Denominators)

Add the tops and leave the bottoms alone:

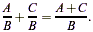
Example:

Add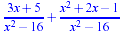

• Subtracting rational expressions with like denominators

Procedure: (Subtracting Rational Expressions with Like Denominators)

Subtract the tops and leave the bottoms alone:

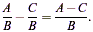
Example:

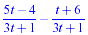
NOTE THE USE OF PARENTHESES IN THE WORK FOR THIS EXAMPLE!!

• Least common multiples and least common denominators.

Recall:

• The least common multiple of a collection of numbers is the smallest number that each of the given numbers is a factor of.

Example:

Find the least common multiple of 9, 12, and 15.

• The least common denominator of a collection of fractions is the least common multiple of the denominators.

Example:

Find a least common denominator for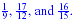

New Stuff:

• The least common multiple (LCM) of a polynomial and least common denominator (LCD) of a rational expression share the same relationship.

Procedure: (Finding the LCD of a collection of rational expressions)

1. Factor each denominator completely.

2. Build the LCM of the denominators as follows:

• Write down the factorization of the first denominator.

• Look at the second denominator and compare it to what you have just written. Write down each factor of the second denominator that does NOT appear in the factorization of the first. (If a factor is the same, but appears more times in the second denominator than in the first, then add as many copies of that factor as are necessary.)

• Look at the third denominator (if there is one). Compare it to what you have written so far. Write down each factor of the third denominator that does not yet appear in the written list of factors.

• Repeat the last step for every remaining denominator, until all have been accounted for.

• When you are done, the LCM should contain each factor the greatest number of times that it occurs in any one denominator.

3. The LCD is the LCM of the denominators.

4. “Fix” the rational expressions by multiplying the top and bottom of each by any factors of the LCD which do not appear in the original denominator.

Example:

Find equivalent expressions which have the LCD for each of the following collections of rational expressions.
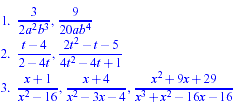