The Slope of a Line
Example 1
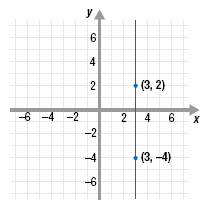
Find the slope of the line that passes through the points (3, 2) and (3, -4).
Solution
| Let (x1, y1) = (3, 2) and (x2, y2)
= (3, .4). |
m |
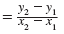 |
| Substitute these values in the slope formula. |
|
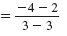 |
| Simplify. |
|
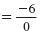 |
| Since division by zero is undefined, the slope is undefined. In fact, the slope of any vertical line is undefined. |
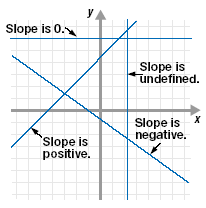
Slope of a Line
| • Slope is positive: Line slants
upward as we move from left to
right.
• Slope is negative: Line slants
downward as we move from left
to right.
• Slope is zero: The slope of a
horizontal line is 0.
• Slope is undefined: The slope
of a vertical line is undefined. |
 |
We can use slope to help us construct the graph of a line.
Example 2
Graph the line that passes through the point (-5, 6) with slope
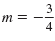 . .
Solution
First, plot the given point, (-5, 6).
To find another point on the line, use the slope. The slope,
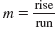 , tells us how to move up and down (rise) and left and right (run) to get to
another point on the line. The slope , tells us how to move up and down (rise) and left and right (run) to get to
another point on the line. The slope
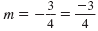 says to move 3 units
down and 4 units right to get to another point, (-1, 3). says to move 3 units
down and 4 units right to get to another point, (-1, 3).
Plot the point (-1, 3).
Finally, draw a line through the two points.
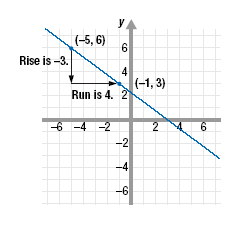
|
