Composition of Functions
Next, we will evaluate the composition of two functions for a given
number using the same two methods that we used previously.
Here is an example using Method 1. That is, we will first find the
composition of the functions and then evaluate the composition for a
specific value of x.
Example 1
Given f(x) = x2 - 9 and g(x)
= x + 5, find (f
○ g) when x = 3. That is, find (f
○ g)(3)
= f[g(3)].
Solution
| Step
1 |
Find (f
○ g)(x).
Replace g(x) with x = 5.
In f(x), replace x with x = 5.
Square the binomial.
Combine like terms.
So, (f
○ g)(x)
= x2 + 10x - 16. |
(f
○ g)(x) |
= f[g(x)] = f[x
+ 5]
= (x + 5)2 - 9
= x2 + 5x + 5x + 25 - 9
= x2 + 10x - 16 |
| Step 2 |
Use x = 3 to find (f
○ g)(3).
Substitute 3 for x.
Simplify. |
|
= (3)2 +
10(3) - 16
= 23 |
So, (f
○ g)(3)
= 23.
Now, let’s use Method 2 to evaluate the composition of two functions.
Here, we will first evaluate the innermost function for a specific value of x.
Then, we will use that result in the outermost function to find the
composition.
Example 2
Given f(x) = x2 - 17 and
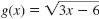 , find (f
○ g) when x
= 5. That is, find (f
○ g)(5)
= f[g(5)].
Solution
| Step
1 |
Use x = 5 to find g(5). Substitute 5 for x in g(x).
Simplify. |
g(5) |
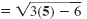
= 3 |
| Step 2 |
Use the result of step 1 in
the function f(x).
Substitute 3 for x in f(x).
Simplify. |
f(x)
f(3)
|
= x2 - 17
= 32 - 17
= -8 |
So, (f
○ g)(5)
= -8.
|
