Solving Quadratic Equations by Completing the
Square
Example
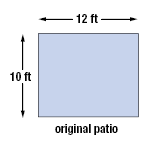
A rectangular patio is 12 feet long and 10 feet wide. We want
to increase the length and the width so the area of the new patio will be
twice that of the original patio. The length will be increased by twice the
amount that the width is increased. By how much should we increase each
dimension?
Solution
| Calculate the area of the original patio.
The area of the new patio will be twice
that of the original patio. |
original area
new area |
= (12 feet)(10 feet)
= 120 ft2 = 2 · 120 ft2
= 240 ft2 |
| Let x = the number of feet the width should be increased. |
| To represent the new width, add x to
the original width.
Since the length will be increased by
twice as much as the width, to
represent the new length, add 2x to
the original length. |
new width
new length |
= 10 + x ft
= 12 + 2x ft |
| The area of the rectangle is:
Area = (length)(width)
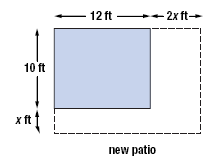 |
| Now, write an equation for the
area of the new patio.
Substitute the expressions.
Multiply the binomials.
Simplify. |
new area
240
240
240 |
= (new length)(new width) = (12 + 2x)(10
+ x)
= 120 + 12x + 20x + 2x2
= 120 + 32x + 2x2 |
| This quadratic equation can be solved by
completing the square. Step 1 Isolate the x2-term and the x-term
on one side of the equation.
Subtract 120 from both sides.
|
120 |
= 32x + 2x2 |
| Write the equation with decreasing
powers of x on the left. |
2x2 + 32x |
= 120 |
| Step 2 If the coefficient of x2 is not 1,
divide both sides of the equation
by the coefficient of x2.
The coefficient of x2 is 2.
Divide both sides of the equation by 2. |
x2 + 16x |
= 60 |
Step 3 Find the number that completes
the square: Multiply the coefficient
of x by
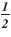 . Square the result. . Square the result.
The coefficient of the x-term is 16.
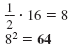
Step 4 Add the result of Step 3 to both
sides of the equation. Add 64 to both sides of the equation. |
x2 + 16x + 64 |
= 60 + 64 |
| Step 5 Write the trinomial as the square
of a binomial.
Write x2 + 16x + 64 as the square of
a binomial.
Also, simplify the right side of the equation. |
(x + 8)2 |
= 124 |
| Step 6 Finish solving using the
Square Root Property.
Use the Square Root Property.
For each equation, subtract 8
from both sides.
Step 7 Check each solution.
We leave the check for you. |
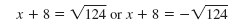
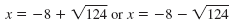
|
You can simplify the radical:
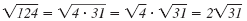
So the solutions are:
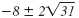
|
