Using the Rules of Exponents
All of the rules for exponents hold for rational exponents as well as integral
exponents. Of course, we cannot apply the rules of exponents to expressions that are
not real numbers.
Rules for Rational Exponents
The following rules hold for any nonzero real numbers a and b and rational
numbers r and s for which the expressions represent real numbers.
| 1. aras = ar+s |
Product rule |
2.
 |
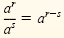Quotient rule |
| 3. (ar)s = ars |
Power of a power rule |
| 4. (ab)r = arbr |
Power of a product rule |
5.
 |
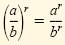Power of a quotient rule |
We can use the product rule to add rational exponents. For example,
161/4 · 161/4 = 162/4.
The fourth root of 16 is 2, and 2 squared is 4. So 162/4 = 4. Because we also have
161/2 = 4, we see that a rational exponent can be reduced to its lowest terms. If an
exponent can be reduced, it is usually simpler to reduce the exponent before we
evaluate the expression. We can simplify 161/4 · 161/4 as follows:
161/4 · 161/4 = 162/4 = 161/2 = 4
Example 1
Using the product and quotient rules with rational exponents
Simplify each expression.
a) 271/6 · 271/2
b)
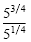
Solution
| a) 271/6 · 271/2 |
= 271/6 + 1/2 |
Product rule for exponents |
| |
= 272/3 |
|
| |
= 9 |
|
b)
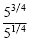= 53/4-1/4 = 52/4 = 51/2 |
We used the quotient rule to subtract the exponents. |
Example 2
Using the power rules with rational exponents
Simplify each expression.
a) 31/2 · 121/2
b) (310)1/2
c)
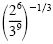
Solution
a) Because the bases 3 and 12 are different, we cannot use the product rule to add
the exponents. Instead, we use the power of a product rule to place the 1/2 power outside the parentheses:
31/2 · 121/2 = (3 · 12)1/2 = 361/2
= 6
b) Use the power of a power rule to multiply the exponents:
(310)1/2 = 35
 |
 |
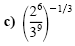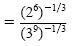Power of a quotient rule |
| |
 |
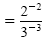Power of a power rule |
| |
 |
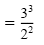Definition of negative exponent |
| |
 |
|
|
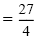