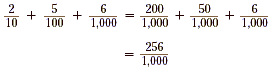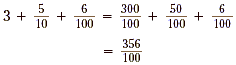Writing Decimals as Fractions

Objective Reinforce your understanding of the meaning of decimal notation as an equivalent form for fractions with a power of 10 in their denominator.

This lesson consists of reinforcement of students’ understanding of the decimal expansion. This is a good opportunity to correct any misunderstandings they may have about decimal expansion.

Decimal Notation

In a decimal, each digit to the right of the decimal point represents a fractional value with a denominator that is a power of 10 (10, 100, 1,000, …). For example, the value represented by the digit 2 in 0.256 is "two tenths". The values represented by the digits 5 and 6 are “five hundredths” and “six thousandths”, respectively. This means the decimal 0.256 can be represented by the sum .

Example 1

Represent 0.78 as the sum of fractions whose denominators are powers of 10.

Solution

0.78 is equivalent to the sum .

It is only the digits to the right of the decimal point that are represented by fractions in a decimal expansion. The digits to the left of the decimal point represent the whole-number part of the decimal.

Example 2

Write 3.56 as a sum involving fractions whose denominators are powers of 10.

Solution

3.56 can be represented by the sum .

Writing Decimals as Fractions

We can write the fractional parts of a decimal expansion as a single fraction by writing them using a common denominator.

Example 3

Write 0.256 as a single fraction.

Solution

As shown previously, we know that 0.256 =

The common denominator for these fractions is 1,000.

So, 0.256 is equivalent to the fraction .

Example 4

Write 3.56 as a single fraction.

Solution

In Example 2, it was shown that . Since , the common denominator is 100.

So, 3.56 is equivalent to .

Alternately, we could add just the fractions in the decimal expansion , and get a mixed number as our result.

So the decimal 3.56 is also equivalent to the mixed number .

Although it is easy to give a simple step-by-step procedure for writing a decimal as a fraction, it is important to do examples of the kind we have just done so that you can see why the procedure works.

Writing Decimals as Fractions

1. Count the number of digits to the right of the decimal point in the given decimal.

2. Drop the decimal point from the decimal, and place the resulting whole number in the numerator of the fraction.

3. In the denominator, write the power of 10 that has as many zeros as there were digits to the right of the decimal point in the given decimal.

Example 5

Write 0.638 as a fraction.

Solution

Step 1 The number of digits to the right of the decimal point is 3.

Step 2 Dropping the decimal point gives the whole number 638. Use this number as the numerator of the fraction.

Step 3 From Step 1, we know that the power of 10 used in the denominator should have 3 zeros. So 1,000 is the denominator of the fraction.

Example 6

Write 21.67 as a fraction and a mixed number.

Solution

Step 1 The number of digits to the right of the decimal point is 2.

Step 2 Dropping the decimal point gives the whole number 2,167. Use this number as the numerator of the fraction.

Step 3 The denominator of the fraction should be 100.

As a mixed number, .