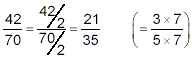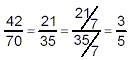Reducing Numerical Fractions to Simplest Form

To reduce a numerical fraction to simplest form means to rewrite it as an equivalent fraction which has the smallest possible denominator. People refer to this operation as reducing a fraction to lowest terms.

Recall that starting with a fraction, we can get an equivalent fraction by either:

(i) multiplying the numerator and denominator by the same nonzero value

or

(ii) dividing the numerator and denominator by the same nonzero value.

Obviously if the goal of simplification is to find an equivalent fraction with a smaller denominator, we will have to use the second principle: dividing the numerator and denominator by the same nonzero value.

The strategy for finding the values to divide into the numerator and denominator is quite systematic:

Step 1: Factor both the numerator and denominator into a product of prime factors using the method described in the previous note in this series.

Step 2: If the numerator and denominator both have a prime factor which is the same, then divide the current numerator and denominator by that value. The result will be the numerator and denominator of an equivalent fraction, but with a smaller denominator.

Repeat step 2 as often as possible. When the numerator and denominator have no further prime factors in common, they form the desired equivalent fraction which has the smallest denominator. We have then obtained the simplest form of the original fraction.

Example:

Reduce the fraction to simplest form.

solution:

For this example, we’ll go through the process step-by-step in some detail. Then we’ll illustrate the familiar “shortcuts” in a couple of examples.

The prime factorizations of the numerator and denominator here are easily obtained:

42 = 2 × 21 = 2 × 3 × 7

70 = 2 × 35 = 2 × 5 × 7

So, the numerator and denominator of the fraction we are given both contain the prime factor 2.

Thus

The new fraction, 21 / 35 , is simpler than the old fraction, 42 / 70 , because its denominator, 35, is smaller than the original denominator of 70. Still, 21 / 35 is equivalent to 42 / 70 because it was obtained by dividing both the numerator and denominator of 42 / 70 by the same value, 2.

But 21 / 35 is still not in simplest form because the factorization of its numerator and denominator (shown in brackets above) indicates that they both still contain a common prime factor of 7. So

Thus, we have

These two fractions, the original 42 / 70and the final 3 / 5 , are equivalent because we got 3 / 5 by dividing the numerator and denominator of 42 / 70 by the same values (2 and 7 in turn, or effectively, 14, if you think of doing it in one step). Furthermore, the numerator and denominator of 3 / 5clearly do not share any further common prime factors, and so this simplification process cannot be carried further. Therefore,

3 / 5 is the simplest form of 42 / 70 .

Example:

Reduce the fraction to simplest form.

solution:

Yes! This is the same problem as the first one. What we want to do here is show the “shortcut” form of the strategy for simplifying fractions. We begin as before by rewriting both the numerator and the denominator as a product of prime factors:

Now, if you study the steps of the previous example, you will see that dividing the numerator and denominator by 2 results in those two factors disappearing from each. We indicate this by drawing “slashes” through them:

Dividing the numerator and denominator in the resulting factored equation by 7 again just results in those two factors of 7 disappearing from each. So again,

Now there are no common factors left in the numerator and denominator, so the process ends, and we conclude that 3 / 5 is the simplest form of 42 / 70 .

In practice, this whole process is typically done in a single step, crossing out pairs of factors without rewriting intermediate forms: