Solving Quadratic Equations
Example
Figure 1 shows the graph of a quadratic function. Find the formula for this quadratic
function and express the formula in vertex form and in standard form.
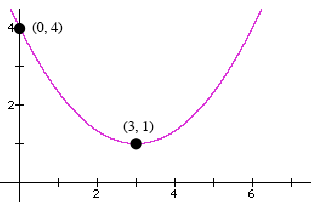
Figure 1: Find the formula of this quadratic function.
Solution
We will find the formula in vertex form (this is relatively easy as the x- and y-coordinates
of the vertex are given) and then convert the vertex form to standard form.
The vertex form of a quadratic function has the format:
y = a · (x - h) 2 + k,
where the letter h represents the x-coordinate of the vertex and the letter k represents the
y-coordinate of the vertex.
Figure 1 shows that the x-coordinate of the vertex is equal to 3 and that the y-coordinate
of the vertex is equal to 1. This means that the vertex form of this quadratic will be:
y = a · (x - 3) 2 +1.
All that remains is to find the numerical value of the constant a. To do this, you can use
the x- and y-coordinates of any other point (i.e. other than the vertex) that lies on the
quadratic – for example the point (0, 4) shown in Figure 3. To work out the value of a
we will plug x = 0 and y = 4 into the vertex form and then solve for a.
4 = a · (0 - 3) 2 +1.
4 = a · 9 +1.
3 = a · 9.
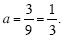
So, the equation for the quadratic function shown in Figure 1 (expressed in vertex form)
is:
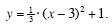
To convert this equation from vertex form to standard form, you can expand by FOILing
and then collect like terms.
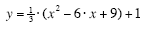 (Expand the (x – 3)2 by FOILing) (Expand the (x – 3)2 by FOILing)
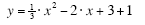 (Multiply through by one third) (Multiply through by one third)
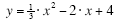 (Combine the like terms) (Combine the like terms)
So, the equation for the quadratic function shown in Figure 1 (expressed in standard
form) is:
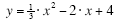
|
