Square Roots
Definition of Square Root
Before we define the square root of a number, let’s review what we mean
by the square of a number.
• The square of 5 is 52, which is 25.
• The square of -5 is (-5)2, which is also 25.
Now we will reverse the squaring process and obtain the square roots of a
number.
The square root of a number is a number that when multiplied by itself,
gives the original number.
The number 25 has two square roots, -5 and -5. Squaring 5 gives 25,
squaring -5 also gives 25.
Each positive real number has two square roots, one positive and the other
negative.
The positive square root of a number is called the principal square root.
The principal square root of 25 is +5.
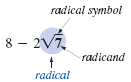
The radical symbol,
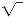 , is used to denote the principle square root of a
number. , is used to denote the principle square root of a
number.
For example,
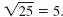
The negative of the radical symbol,
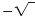 , denotes the negative square
root. , denotes the negative square
root.
For example,
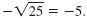
Note:
The number 0 has a single square root, 0.
A negative real number, for example -25,
does not have square roots that are real
numbers. That’s because a real number
times itself always gives a nonnegative
number.
The expression under the radical symbol is called the radicand.
For example, in the expression
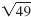 , the radicand is 49. , the radicand is 49.
A radical is the part of an expression that consists
of a radical symbol and a radicand. In this
example, the radical is
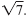
A radical expression is an expression that
contains a radical.
|
