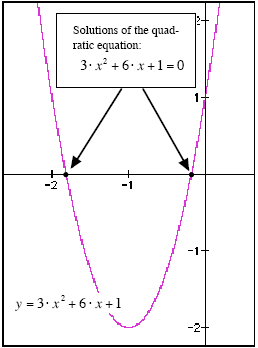
Evaluating the Quadratic Formula

Solving a Quadratic Equation Graphically

From a graphical point of view, the solutions of a quadratic equation like: 

3· x ² + 6 · x +1= 0

are the x-coordinates of the points where the graph o f  y = 3· x ² + 6 · x +1 cuts through the x-axis

(see Figure 1).

Figure 1: The solutions of a quadratic are the xcoordinates of the points where the graph cuts the x-axis.

You can locate these points (at least approximately) by using a graphing calculator.

Solving a Quadratic Equation Algebraically

The key difficulty in using a graphing calculator to solve a quadratic equation (in fact, the main problem in using a graphing calculator to solve any equation) is that you need to set the viewing window so that you can see the points where the quadratic graph cuts through the x-axis. Unless you happen to know about where these points will be, setting the viewing window to show them is a hitand- miss, trial-and-error procedure.

As with many of the other equations that we have studied, it is possible to solve a quadratic equation using algebra. Using algebra to solve a quadratic equation avoids the problem of guessing a good size for the viewing window and is often easier because of this. 

Using Factoring to Solve a Quadratic Equation

Unless the numbers are chosen to be very nice, factoring a quadratic equation can be very hard or impossible. However, when you are able to factor a quadratic, the factored form makes it very easy for you to find the solutions of the quadratic equation.

Example

Find all solutions of the quadratic equation: 

x ² + 8 · x +10 = 30.

Solution

First note that solving this quadratic equation is the same as solving the quadratic equation: 

x ² + 8 · x +10 - 30 = 30 - 30 (Subtract 30 from each side) 

x ² + 8 · x - 20 = 0 (Simplify)

Solving the quadratic equation  x² + 8 · x - 20 = 0 will give exactly the same values for x that solving the original quadratic equation,  x² + 8 · x +10 = 30, will give.

To factor the quadratic, you have to find a pair of numbers that add to give +8 and which multiply to give -20. Two numbers that do this are +10 and -2. So you can write the quadratic equation in factored form as: 

(x - 2) · (x +10) = 0

The two x-values that will satisfy this equation are x = 2 and x = -10. The solutions of the quadratic equation:

x² + 8 · x +10 = 30

are x = 2 and x = -10.

Using Vertex Form to Solve a Quadratic Equation

If you happen to have a quadratic equation where the quadratic part of the equation is already expressed in vertex form, then you can solve the quadratic equation in a reasonably straightforward manner.

If the quadratic part of your quadratic equation is not already expressed in vertex form, then you can convert it to vertex form by completing the square. Completing the square can be quite a complicated process, however, so solving a quadratic equation that is not already in vertex form can be quite an undertaking.