Algebra Tutorials!



	Home
	About Us
	TUTORIALS:
	Absolute Values
	Solving Two-Step Equations Algebraically
	Multiplying Monomials
	Factoring Trinomials
	Solving Quadratic Equations
	Power Functions and Transformations
	Composition of Functions
	Rational Inequalities
	Equations of Lines
	Graphing Logarithmic Functions
	Elimination Using Multiplication
	Multiplying Large Numbers
	Multiplying by 11
	Graphing Absolute Value Inequalities
	Polynomials
	The Discriminant
	Reducing Numerical Fractions to Simplest Form
	Addition of Algebraic Fractions
	Graphing Inequalities in Two Variables
	Adding and Subtracting Rational Expressions with Unlike Denominators
	Multiplying Binomials
	Graphing Linear Inequalities
	Properties of Numbers and Definitions
	Factoring Trinomials
	Relatively Prime Numbers
	Point
	Inequalities
	Rotating a Hyperbola
	Writing Algebraic Expressions
	Quadratic and Power Inequalities
	Solving Quadratic Equations by Completing the Square
	BEDMAS & Fractions
	Solving Absolute Value Equations
	Writing Linear Equations in Slope-Intercept Form
	Adding and Subtracting Rational Expressions with Different Denominators
	Reducing Rational Expressions
	Solving Absolute Value Equations
	Equations of a Line - Slope-intercept form
	Adding and Subtracting Rational Expressions with Unlike Denominators
	Solving Equations with a Fractional Exponent
	Simple Trinomials as Products of Binomials
	Equivalent Fractions
	Multiplying Polynomials
	Slope
	Graphing Equations in Three Variables
	Properties of Exponents
	Graphing Linear Inequalities
	Solving Cubic Equations by Factoring
	Adding and Subtracting Fractions
	Multiplying Whole Numbers
	Straight Lines
	Solving Absolute Value Equations
	Solving Nonlinear Equations
	Factoring Polynomials by Finding the Greatest Common Factor
	Logarithms
	Algebraic Expressions Containing Radicals 1
	Addition Property of Equality
	Three special types of lines
	Quadratic Inequalities That Cannot Be Factored
	Adding and Subtracting Fractions
	Coordinate System
	Solving Equations
	Factoring Polynomials
	Solving Quadratic Equations
	Multiplying Radical Expressions
	Solving Quadratic Equations Using the Square Root Property
	The Slope of a Line
	Square Roots
	Adding Polynomials
	Arithmetic with Positive and Negative Numbers
	Solving Equations
	Powers and Roots of Complex Numbers
	Adding, Subtracting and Finding Least Common Denominators
	What the Factored Form of a Quadratic can tell you about the graph
	Plotting a Point
	Solving Equations with Variables on Each Side
	Finding the GCF of a Set of Monomials
	Completing the Square
	Solving Equations with Radicals and Exponents
	Solving Systems of Equations By Substitution
	Adding and Subtracting Rational Expressions
	Percents
	Laws of Exponents and Dividing Monomials
	Factoring Special Quadratic Polynomials
	Radicals
	Solving Quadratic Equations by Completing the Square
	Reducing Numerical Fractions to Simplest Form
	Factoring Trinomials
	Writing Decimals as Fractions
	Using the Rules of Exponents
	Evaluating the Quadratic Formula
	Rationalizing the Denominator
	Multiplication by 429
	Writing Linear Equations in Point-Slope Form
	Multiplying Radicals
	Dividing Polynomials by Monomials
	Factoring Trinomials
	Introduction to Fractions
	Square Roots

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Elimination Using Multiplication

Multiplying Both Equations to Simplify the System

For some systems of equations, one equation must be multiplied by a fraction in order to make elimination by addition or subtraction possible. Since multiplication of integers is easier, both equations are multiplied by nonzero numbers so that the coefficients of a variable in the equations become equal (or opposite).

Example 1

Solve the system of equations.

2x + 9y = 7

3x + 7y = 4

Solution

One approach is to multiply the first equation by 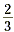, and then subtract the resulting equation from the second one. This method works, but involves fractional arithmetic. Another approach is to multiply the first equation by 3 and the second by 2, to get an equivalent system of equations.

3(2x + 9y = 7 )	6x + 27y = 21
2(3x + 7y = 4 )	6x + 14y = 8
	6x + 27y = 21
	( - ) 6x + 14y = 8	Subtract the equations.
	0 + 13y = 13
	13y = 13
	y = 1	Divide each side by 13.

Now substitute 1 for y in the second equation.

6x + 14y = 8
6x + 14(1) = 8	Replace y with 1.
6x = -6
x = -1

The solution is ( -1, 1).