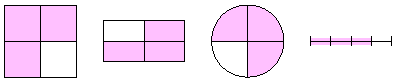| Algebra Tutorials! |
Introduction to FractionsWhat Fractions Are and Why They Are ImportantA fraction can mean part of a whole. Just as a whole number answers the question, How many?, a fraction answers the question, What part of? Every day we use fractions in this sense. For example, we can speak of two-thirds of a class (meaning two of every three students) or three-fourths of a dollar (indicating that we have split a dollar into four equal parts and have taken three of these parts). A fraction can also mean the quotient of two whole numbers. In
this sense, the fraction Definition A fraction is any number that can be written in the form Explain why in this definition b cannot be 0. From this definition, When written as
Alternatively, a fraction can be represented as either a decimal or a percent. Fraction Diagrams and Proper FractionsDiagrams help us work with fractions. Each diagram represents
the fraction three-fourths, or
Note that in each diagram the whole has been divided into 4 equal parts, with 3 of the parts shaded. The number Explain why a fraction whose numerator is smaller than its denominator must have a value less than 1. EXAMPLE 1 What fraction does the diagram represent?
Solution In this diagram, the whole is divided into 9 equal parts, so
the denominator of the illustrated fraction is 9. Four of these
parts are shaded, so the numerator is 4. The diagram illustrates
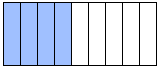
the fraction PRACTICE 1 The diagram illustrates what fraction?
Answer
EXAMPLE 2 A manufacturing company plans to lay off 71 of its 230 workers. What fraction of its employees does the company plan to lay off? Solution There are 230 workers altogether, so the denominator of our
fraction is 230. Because we are concerned with 71 of these
workers, 71 is the numerator. The company plans to lay off PRACTICE 2 The annual tuition at a college is $2,451. If a student paid $1,000 toward this tuition, what fraction of the tuition did the student pay? Answer
EXAMPLE 3 The U.S. Senate approved a foreign aid spending bill by a vote of 83 to 17. What fraction of the senators voted against the bill? Solution First, we find the total number of senators. Because 83
senators voted for the bill and 17 voted against it, the total
number of senators is 83 + 17, or 100. So PRACTICE 3 You have read 125 pages of a novel assigned by your English instructor. If 39 pages remain, what fraction of the book have you read? Answer
|
tells us what we get when we divide the
whole number 3 by the whole number 4. 
, where a
and b are whole numbers and b is not zero. 
are all fractions. 
. 
of its
employees. 
of the
senators voted against the bill. 
